Play is an essential way to learn about the world. Doing activities we love without a specific goal allows us to discover new information, better understand our own abilities, and find unexpected beauty around us. Arithmetic is an example of an area we can explore through play.
Every parent knows that children need space for unstructured play, which helps them develop their creativity and problem-solving skills. Free experiments lead to the rapid acquisition of information about the world. When children play together, they develop their social skills and strengthen their ability to regulate their emotions. Young animals, such as elephants, dogs, crows and crocodiles, also develop survival skills through play.
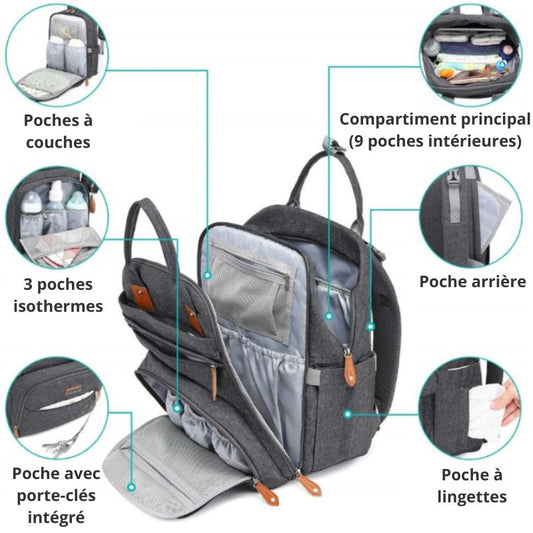
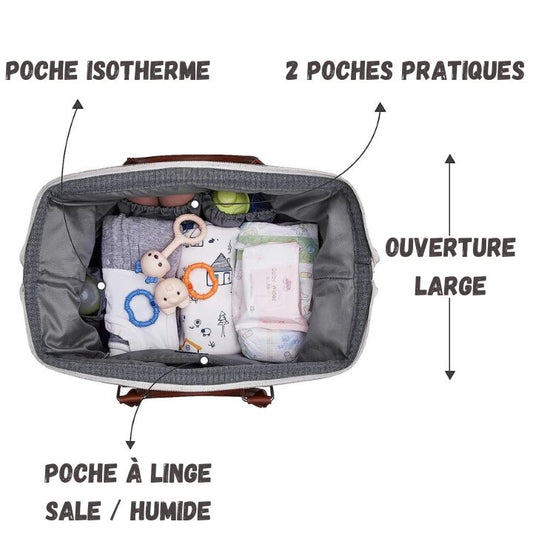
Discover our Moms & Kids collection.
The benefits of gambling don't disappear once you become an adult. Even though we engage our curiosity in different ways as we grow up, a lot of learning and exploration still comes from analogous activities: things we do simply for fun.
When the pressure is on to be productive every minute of the day, we have a lot to gain from doing everything we can to find time to play. By removing prescriptions and obligations, we move towards what interests us most. Just like children and baby elephants, we can learn important lessons through play. It can also give us a new perspective on topics we take for granted—like how we represent numbers.
Play with symbols
The book Arithmetic , in addition to being a clear and engaging history of the subject, demonstrates how intuitions and understanding can be combined with pleasure and amusement. The best place to start the book is with the afterword, where author and mathematics professor Paul Lockhart writes: “Most of all, I hope I've succeeded in conveying the idea of seeing your mind as a playground—a place to create beautiful things for your own pleasure and amusement and to marvel at what you have created and what you have yet to understand. »
Arithmetic, the branch of mathematics that deals with the manipulation and properties of numbers, can be very fun. After all, there are many ways to add and multiply numbers that can themselves be represented in different ways. When we see six cows in a field, we represent this quantity with the symbol 6. The Romans used VI. And there are many more ways that unfortunately cannot be typed on a standard English keyboard. If two more cows enter the field, the usual method of counting them is to add 2 to 6 and conclude that there are now 8 cows. But we could just as easily add 2 + 3 + 3. Or turn everything into fractions with a base of 2 and go from there.
One of the most intriguing parts of the book is when Lockhart encourages us to move away from the way we usually label numbers so that we can have fun experimenting with them. He says: “The problem with familiarity is not so much that it breeds contempt, but that it breeds loss of perspective. » Lest we get too hung up on our symbols like 4 and 5, Lockhart shows us how any symbols can be used to accomplish some of the major arithmetic tasks like comparing and grouping. It shows how completely random symbols can represent quantities and provides insight into how they can be manipulated.
When we start playing with representations, we connect to the reasoning behind what we are doing. We might count for purposes of comparison, and we might also be interested in learning the patterns produced by our actions. Lockhart explains that “each number can be represented in different ways, and we want to choose a form that is as useful and practical as possible. » So we can choose our representations of numbers based on curiosity rather than what is conventional. It’s easy to extrapolate this thought to broader life situations. How often do we assume that certain parameters are fixed simply because that's what has always been done? What else could we accomplish if we abandoned convention and focused instead on function?
Moving away from requirements
We all use the Hindu-Arabic numbering system, which uses groups of ten. Ten ones makes ten, ten tens makes one hundred, and so on. It has a coherent logic, and it's a ubiquitous way of grouping numbers as they increase. But Lockhart explains that grouping numbers by ten is as arbitrary as the symbols we use to represent numbers. He explains how a society might group in fours or sevens. One of the most interesting ideas, however, comes when he explains the groupings:
“You might think there’s no question about that; we chose four as the grouping size, so that's how it is. Of course, we'll group our groups into four—as opposed to what? Group things into four and then group our groups into six? That would be insane! But it happens all the time. Inches are grouped into twelve to make feet, and then three feet make a yard. And the old British monetary system had twelve pence per shilling and twenty shillings per pound. »
By reminding us of the options available in such a simple, everyday activity as counting, Lockhart opens a mental door. What other ways could we approach our tasks and solve our problems? It reminds us that most of our so-called demands are ones we impose on ourselves.
If we think back to our childhood, we often played with things in a different way than they were intended. Pots became drums and duct tape wrapped around the house became lasers. A byproduct of this type of play is usually learning—we learn what things are normally used for by playing with them. But that is not the intention behind a child's play. Pleasure comes first, and so they do not restrict themselves to convention.
Have fun with the unknown
There are advantages and disadvantages to all counting systems. For Lockhart, the only way to find out what they are is to play with them. And it is by playing that we can learn more than arithmetic. For example, he says: “Actually, being stuck (say on 7+8) is one of the best things that can happen to you because it gives you the opportunity to reinvent and enjoy exactly what you're doing. » In the case of adding two numbers, we "rearrange the numerical information for comparison." »
The main point is that getting stuck on anything can be incredibly helpful. It forces you to stop and think about what you're really trying to accomplish. Being stuck can help you identify first principles in your situation. By unblocking yourself, we learn lessons that resonate and help us grow.
Lockhart says of arithmetic that we must "not let our familiarity with a particular system blind us to its arbitrariness." » We don't need to use the symbol 2 to represent how many cows there are in a field, just like we don't need to group sixty minutes into an hour. We may find these representations useful, but we may also not find them useful. Some people in the world have so much money that the numbers representing their wealth are almost insane, and most people find the clock manipulation of the annual switch to daylight saving time annoying and stressful.
Playing with arithmetic can teach the broader lesson that we don't have to continue using systems that no longer serve us well. Yet how many of us find it difficult to let go of what is ineffective simply because it is familiar?
This brings us back to play. Play is often the exploration of the unknown. After all, if you knew what the outcome would be, it probably wouldn't be considered gambling. When we play, we take risks, we experiment, and we try new combinations just to see what happens. We do all of this in pursuit of pleasure because it is the novelty that brings us pleasure and makes the game rewarding.
Lockhart makes a similar point about arithmetic:
“ The purpose of studying arithmetic and its philosophy is not only to become good at arithmetic but also to gain a broader perspective and broaden our view of the world... Moreover, it is amusing. Regardless, as arithmetic geeks, we should always question and criticize, examine and play. »
Have fun with numbers
We suggest that the game is not limited to arithmetic. If you like playing with numbers, then go for it. Lockhart's book offers great inspiration on how to have fun with numbers. Play is inherently valuable and does not need to be productive. Children and animals have no purpose for play; they just do what's fun. It turns out that unstructured, undirected play often has incredibly powerful byproducts.
Play can lead to new ideas and innovations. It can also lead to personal growth and development, not to mention a better understanding of the world. And, by definition, play leads to pleasure. Which is the best part. Arithmetic is just one example of an unexpected area that we can approach with a playful spirit. For more information on the benefits of play for children, visit UNICEF .